60 yıllık problemi çözdü! 100 sayfalık kanıt yayınladı
60 Yıllık Matematik Problemi Sonunda Çözüldü!
Bu zorlu matematik problemi, ilk kez 1966 yılında Avusturya-Kanadalı matematikçi Leo Moser tarafından gündeme getirildi. 1 birim genişliğindeki bir koridorda, L şeklindeki bir köşeden geçebilecek en geniş koltuğun boyutu konusu, yıllarca matematikçilerin zihnini meşgul etti.
1968 yılında ise İngiliz matematikçi John Hammersley, yarım daire ve bir kareyi birleştirerek 2.2074 birimlik bir çözüm buldu. Ancak Hammersley, tasarım için belirlediği üst sınırla da dikkat çekti; 2,8284’ten büyük hiçbir şeyin geçemeyeceğini savundu.
1992’de Rutgers Üniversitesi’nden Joseph Gerver, Hammersley’in tasarımını geliştirerek yuvarlak kenarlarla daha uygun bir çözüm öne sürdü ve 2.2195 birimlik bir koltuğun en iyi çözüm olduğunu iddia etti, ancak bu çözümün genel geçer bir kanıtı henüz bulunamamıştı.
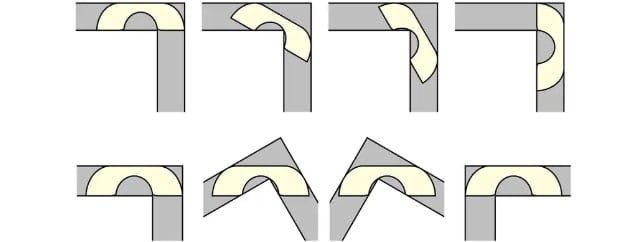
2018’de Santa Fe Enstitüsü’nden Yoav Kallus ve Kaliforniya Üniversitesi’nden Dan Romik, bilgisayar destekli bir yöntemle bu değerin biraz daha artabileceğini öne sürdü. Ancak kesin kanıt hala net değildi.
Son olarak, Ineon Baek, matematiksel bir yöntem olan “injective function” kullanarak Gerver’in çözümünü sınırladı ve 2.2195 birimin L şeklindeki koridordan geçebilecek en geniş koltuk boyutu olduğunu matematiksel olarak kanıtladı.
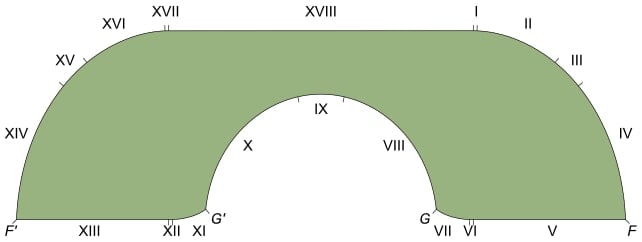
Baek’in çalışması henüz hakem değerlendirmesinden geçmemiş olsa da, matematik camiasında büyük heyecan yarattı. Bu tarihî başarı, 60 yıldır devam eden tartışmayı sona erdirerek koltuk taşıma sorununa net bir çözüm getirdi.
Ancak matematikçiler uyarıyor: Eğer bir köşeyi daha dönmeniz gerekiyorsa, “Romik’in iki yönlü koltuğu” sizin için en iyi seçenek olabilir. Bu koltuğu IKEA’da Gimli’nin mutfak masasının yanında bulabilirsiniz!
